Cálculo del combustible requerido para una propulsión de alunizaje

Considérese éste planteamiento hipotético (tomado y adaptado de la XI Olimpiada Internacional de Física):

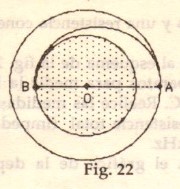
Un vehículo de masa \(m\) se mueve alrededor de la luna en una órbita circular de altura \(h\). Para descender a una órbita de alunizaje, se conecta un motor durante un intervalo corto de tiempo. La velocidad de escape de los gases del motor es \(u\). El radio de la luna es \(r_L\) y la aceleración de la gravedad lunar es \(g_L\).

Evalúese el gasto de combustible para trasladar a la nave desde la trayectoria inicial \(A\) hasta la superficie del satélite \(B\). 

La órbita describe una circunferencia de \(e=0\) y \(r=r_L+h\). El módulo de su velocidad \(v_0\) invaría, pues la fuerza que le imprime el satélite es uniforme. \(M\) es la cantidad de materia de la luna.

\[ma_c=\frac{GMm}{r^{2}}=\frac{mv_{0}^{2}}{r}\]

\[v_{0}=\sqrt{\frac{GM}{r}}\]

\[GM=r_{L}^{2}g_L\]

\[v_{0}=r_L\sqrt{\frac{g_L}{r}}\]

Para alterar dicho tránsito y alunizar, se ha de emplear una órbita elíptica que, al alcanzar el cambio instantáneo de \(\Delta v=v_0-v_A\), se sirva de la impulsión del combustible. Se sigue que, de la conservación del momento angular, \(v_Ar=v_Br_L\), siendo aquéllas las velocidades en las longitudes máxima y mínima al foco, respectivamente; y, de la conservación de la energía mecánica, que \(\frac{1}{2}mv_{A}^{2}-\frac{GMm}{r}=\frac{1}{2}mv_{B}^{2}-\frac{GMm}{r_L}\).

\[\frac{v_{A}^{2}}{2}-\frac{GM}{r}=\frac{v_{B}^{2}}{2}-\frac{GM}{r_L}\]

\[\frac{v_Ar}{r_L}=v_B\]

\[\frac{v_{A}^{2}}{2}-\frac{v_{A}^{2}r^{2}}{2r_{L}^{2}}=\frac{r_{L}^{2}g_L}{r}-r_{L}g_L\]

\[\frac{v_{A}^{2}}{2}\left ( 1-\left ( \frac{r}{r_L} \right )^2 \right )=g_L\left ( \frac{r_{L}^{2}}{r}-r_L \right )\]

\[v_{A}=r_L\sqrt{2g_L\frac{r_L(r_L-r)}{r(r_{L}^{2}-r^2)}}\]

\[\Delta v=r_L\left (\sqrt{\frac{g_L}{r}}-\sqrt{2g_L\frac{r_L(r_L-r)}{r(r_{L}^{2}-r^2)}}  \right )\]

La anexión del motor ha de remitirse al sistema nave combustible, donde la cantidad de movimiento es conservativa. Sea \(m_1\) la masa del propulsor, se cumple que \(m_1u=\Delta v(m-m_1)\).

\[m_1=m\frac{\Delta v}{u+\Delta v}\]

\(\Delta v\ll u\)

\[m_1=\frac{m}{u}r_L\left (\sqrt{\frac{g_L}{r}}-\sqrt{2g_L\frac{r_L(r_L-r)}{r(r_{L}^{2}-r^2)}}  \right )\]

Comentarios

Publicar un comentario

Entradas populares de este blog

Deducción del principio de gravitación newtoniano

Por definición, acontece que la acción gravitacional recíproca que experimenta un par aislado de corpúsculos es proporcional al producto de sus masas, \(m_1\) y \(m_2\), e inversamente proporcional al cuadrado de la distancia, \(r\), que los separa. Discurre, de este modo, la formulación del principio de gravitación universal newtoniano, que, además, le relaciona una constante \(G\), que concreta la magnitud de esta fuerza atractiva. \[F=G\frac{m_1m_2}{r^2}\] He aquí, se ha de reconstruir el modelo matemático de aquélla proposición, apelando, por ello, a mediciones actuales, que convergen con facilidad en la demostración antedicha. Obtención a partir de las aceleraciones centrípetas de la luna y de una partícula en la superficie terrestre Es evidente que a toda causa motriz corresponde un efecto igual y contrario: O sea, las acciones mutuas de dos cuerpos (\(m_1\),\(m_2\)) siempre son iguales y dirigidas en direcciones opuestas. Concédase, entonces, que el módulo de aquélla fuerza inva
Leer más

Los empiristas británicos

Imagen
Como característica general, los filósofos empiristas enmarcan a la experiencia como legitimadora del conocimiento. Según Descartes, el padre de la modernidad racionalista, existen nociones impresas en el alma, cuyas bases descansan en la formalidad a priori. El empirismo parte de la refutación de aquel innatismo. Según sus principios gnoseológicos, el conocimiento circunda el mundo externo, pues la sensibilidad dibuja sus trazos sobre la mente humana sólo conforme sé es consciente de los datos que aquélla provee. He aquí una síntesis de su pensamiento, que abarca: La refutación de las ideas innatas. El lugar de los principios de la lógica en la experiencia. Dios como la base ontológica de los sistemas del mundo. La negación de la materia como sustrato extrínseco. LA NEGACIÓN DEL INNATISMO John Locke Grabado de John Locke. La inexistencia de las nociones primarias, fundamentales, irreductibles, sustanciales y de predeterminación natural a las que la tradición filosófica llam
Leer más